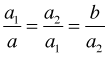
Descartes's curve for finding two mean proportionals

To find two mean proportionals between two numbers a and b means to find a₁ and a₂ between A and B so that

That is, the four points form a geometric sequence

To solve any such problem geometrically,

1. Use Descartes's linkage machine to trace a curve with point D (shown here in green.)
2. Adjust the point A so that the distance AY = a.
3. Find the point on the horizontal axis so that b = E.
4. Construct a circle whose diameter is YE.
5. Find the intersection point, D, of the curve with the circle. In this applet, you will have to manually move point D so that it lies on the curve.
6. Drop a perpendicular from D to the horizontal axis, intersecting at a point C.
7. The lengths YC and YD are the desired mean proportionals. To mark distance YD on the horizontal axis, use a circle with center A.
   

Use the slider or the "play" button in the lower left corner of the applet window to see the steps just described (though not the initial adjustment of the points.)

The applet is initially set to find two mean proportionals between 1 and 8. Mental arithmetic says they are 2 and 4, and these distances are shown in the diagram. Lengths and ratios are shown in the spreadsheet on the right.

Try some other pairs of numbers, then check the results algebraically.

See Descartes's Logarithm Machine for a full explanation.

Related demonstration files:

Similar right triangles

Geometric means

Descartes's mean proportionals/logarithm machine

Descartes's machine used to solve a "two mean proportionals" problem

Descartes's machine used to plot points on the graph of a logarithm function

Descartes's construction used to find the slope of a tangent to a logarithmic graph

Susan Addington, Created with GeoGebra

Quadrivium

Applets