Measuring the World is a textbook for a mathematics course for future elementary and middle school teachers, written by Susan Addington and David Dennis. The book is a unified course of study based on a foundation of measurement concepts and practices.

Measuring the World covers mathematics commonly taught in U.S. schools through 7th or 8th grade, but from a more sophisticated, teacher's point of view. The topics were chosen to prepare K-8 students for two main purposes: "home economics": the mathematics needed for personal life and citizenship, and to prepare for further work in mathematics.

Most modern math books are about mathematics and its internal structure. However, mathematics was developed to measure and count things in the world; the logical structure of mathematics developed only after the system of mathematics was in place. Most of our current curriculum has lost track of these vital connections, and the experience and intuitions that guide elementary mathematical understanding.

Until fairly recently, most people learned about measuring from family and on the job. Activities in daily life---cooking and sewing, carpentry and gardening, travel and telling time, music and decorative arts---all required measurement. Sometimes precise measurement with tools and units were needed, but often estimating and common sense were more important. In our modern urban technological society, most of our food, clothing, furniture, music, and decorative objects come ready-made; making these things is often just a hobby, and is not done out of economic necessity. Measurements are commonly done digitally, in a way that the physical measurement process is obscured. Children often do not develop the intuitions about measurement, quantities, and units that are the foundation of elementary mathematics.

This book is based on the most recent research in mathematical cognition, especially on multiplicative thinking, measurement, and neuroscience. See References for some fairly nontechnical reading.

Technology is the elephant in the room of contemporary math education. The arithmetic skills which used to be the heart of elementary mathematics teaching can now be performed by a $1 calculator, or the calculator on a cell phone. Most traditional algebra word problems (which are contrived to have nice whole number answers) can be solved easily by educated guessing with a spreadsheet program. Measuring the World integrates technology as a tool for problem solving, and opens the way for a future mathematics curriculum that takes full advantage of modern mathematical technology, in which arithmetic algorithms are studied to build understanding about how numbers work.

Do your students need this book?

Do your students have basic skills and concepts of measurement? Try the diagnostic quiz. It is designed as a written-response test, since the way students approach and answer the questions gives a lot of information about what they understand. The test is fairly easy to score; a scoring guide is available to instructors on request.

Organization and contents

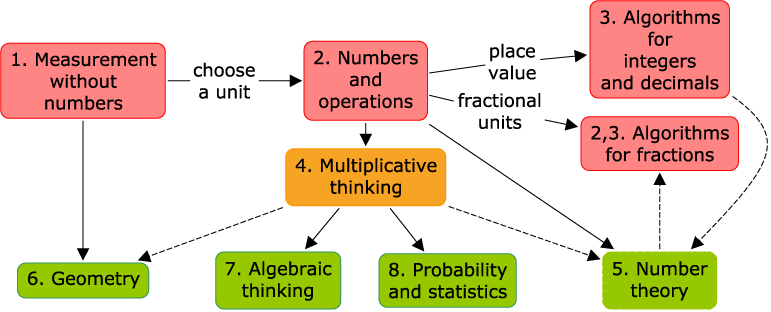
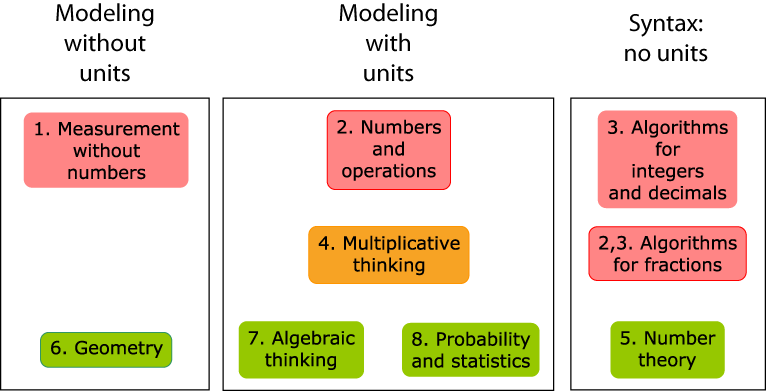
Measuring the World starts with a chapter on measuring (that is, comparing quantities) without units of measurement. Much of geometry also does not use numbers. With the choice of a unit of measure, quantities can be measured more precisely with numbers. This gives rise to various kinds of numbers and operations with these numbers.

Algorithms for computing are then developed after a choice of a system of units. Units in denominations of 10 lead to the place value base 10 system, and our procedures for paper-and-pencil (or abacus) computations for whole numbers and decimals. Fractional units such as 1/3 and 1/4 give rise to the common fractions, with a separate set of computational procedures.

Higher-level mathematical thinking is increasingly about the relations between objects, rather than about the objects themselves. Multiplicative thinking is the missing link between more abstract secondary school topics and the more concrete topics of elementary school. Multiplicative thinking includes thinking about the rules for multiplying and dividing, especially fractions, as well as ratios, proportions, percents, and linear functions. Similarity, area, and volume are topics in other areas that use and develop multiplicative thinking.

The chapter on geometry is not axiomatic; rather, it fills in the extensive background in experimental geometry that students need to be ready for an axiomatic approach in high school. Similarly, algebraic thinking is not about symbolic algebra. Rather, it focuses on elementary functions in context, problem solving, and representations for function/relation situations: tables, graphs, expressions, and arrow diagrams. The chapter on probability and statistics is also focused on experience, and thinking in a statistical manner, rather than a full formal treatment of statistics. Number theory is a bit of a backwater. It is needed for the final touches on fraction arithmetic, such as lowest common denominators. The number theory of positive integers is a model for polynomial algebra, but somehow this is never brought up in most algebra courses.

Flow charts

"Modeling" refers to building mathematical models that include selected features of real-life physical or social situations. For example, the equation D=RT is a model for a car traveling at a constant speed. In real life, cars never travel at a constant speed for an indefinite period, but this equation is good enough for solving many problems. Its simplicity makes it very easy to work with.

Contents

Detailed table of contents

Possible course designs: quarters, semesters, short courses, specialized courses...

Sample sections.

1.2. Comparing areas

2.2. Fractions, part 1

4.3. Ratios

6.3. Angles

Appendix 2: Using spreadsheets for mathematics

Applets

Most of the interaactive applets for this course, as well as some at the secondary and college levels.

The complete book

The book is ready for external pilot testing now, and currently being used in some sections of the courses for elementary teachers at California State University, San Bernardino. Some sections are being reorganized and rewritten.

We plan to distribute this book predominantly in electronic format, with printed versions optionally available through a 3rd party custom printing website.

If you are interested in using this book in your class, or for inservice teacher education, please contact Susan Addington for access to the complete book, ,

While this is a textbook for teachers, not necessarily for children, it does form an outline for a fairly complete curriculum for K-8 students. Contact Susan Addington if you are interested in this direction.

References

Further reading on the topics in this introduction