The interactive diagram requires that you download and install a plugin for Cabri3D. It is free, and runs on Macintosh and Windows (but not Linux.)
How to manipulate a Cabri3D diagram
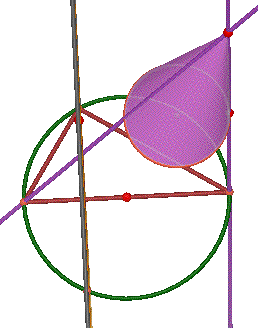
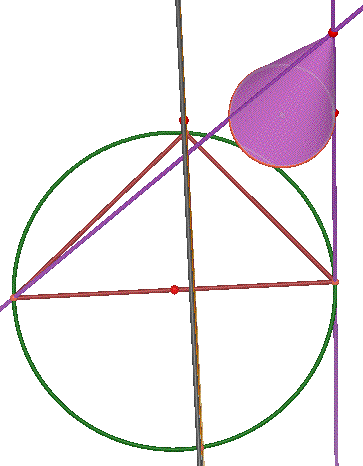
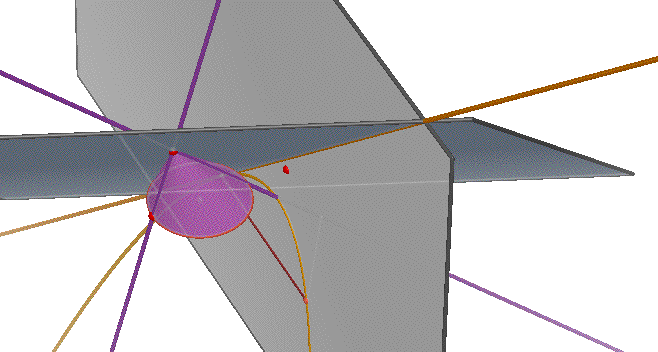
A cone is determined by a circle and a point (the vertex) not in the plane of the circe. A line L through the vertex and a point on a circle sweeps out a cone. In this diagram, only a piece of one of the two parts of the cone is shown so that you can see everything else more clearly. You can change the shape of the cone by moving the vertex.
Any plane parallel to the plane of the original circle cuts the cone in a circle (green.) Adjust the height of the plane with the point labeled "Move circle plane".
Any fixed position of the moving line L that sweeps out the cone determines a tangent plane to the cone (not shown.) Change the line L, and hence the tangent plane direction, by moving the point of tangency along the generating circle (point labeled "Move tangent plane".)
Another plane is also shown. It is defined by L and the center of any one of the circular cross sections. It cuts the cone in two lines (purple) through the vertex, and cuts any cross section circle in a diameter. The similar triangles are important in the derivation of the equation of the parabola.

A plane parallel to the chosen tangent plane cuts the cone in a parabola (gold.) The distance of the section plane from the tangent plane is adjusted with the point labeled "Move parabola plane". When this point is on the other side of the tangent plane, the section plane intersects the invisible upper part of the cone. The parabola is still shown, and opens in the opposite direction.
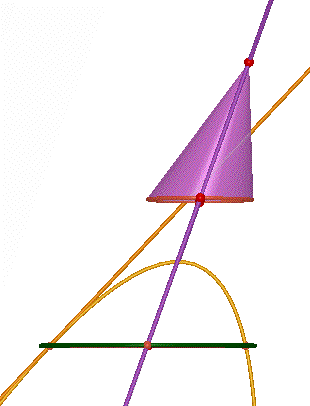
This construction also gives the tangent line to the parabola: it's the intersection of the section plane with the tangent plane to the cone at the point on the parabola. (This tangent plane is not shown in interactive diagram, but here is a screen snapshot.)
By drawing in several line segments, you see the geometric mean picture in the circle plane. The pictures below show two cross sections, the first closer to the vertex than the second. Note how the shape of the triangle changes. (See the lecture notes Sim&GM.pdf and Apollonius.pdf for details of the derivation of the equation.)