Daisy chains of multiplication and division

(You should see a blank window, ready for you to make your own daisy chains. Read directions below.)

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

A daisy chain is a chain of multiplications and divisions, illustrated by arrows. It helps to understand how multiplication and division, especially of fractions, work in combination. The terminology was invented by math cognition researcher Jere Confrey.

For example, the multiplication 2 x 3 = 6 is illustrated by a point for 2, an arrow for the operator of multiplying by 3, ending at a point for the product, 6.

Daisy chain showing 2 x 3 = 6

If you then want to multiply 6 by 4, start another arrow at 6.

Daisy chain showing 2 x 3 x 4 = 24

There are two tools, MultArrow and DivArrow, in this file, at the right end of the tool bar. Pull down on the tiny triangle in the lower right of the Tool button to find them.

What MultArrow and DivArrow tools look like

How to use the tools:
If you are starting a new calculation, click for the beginning point, then click to make another point for the endpoint. Then, in the window that opens, type a number for the beginning number (the first factor).

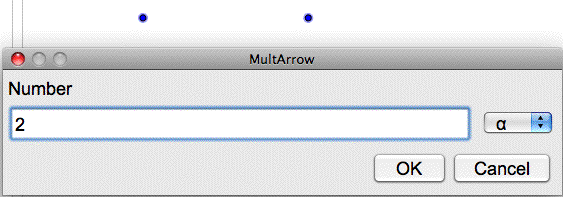
Window to type in first factor

Then, in the next window, type the second factor (the number on the arrow.) When you click OK, the arrow will appear with the input numbers and resulting number (product or quotient) in the correct places.

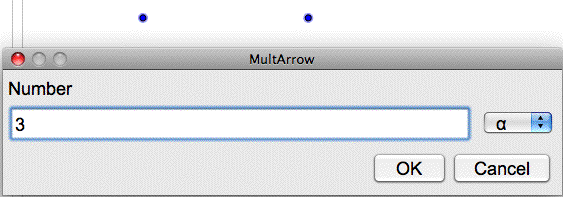
Window to type second factor

To continue a calculation with another arrow, first click the endpoint of an existing calculation to start the next arrow, then click a new point. Instead of typing a new starting number, type the ending number for the previous result.

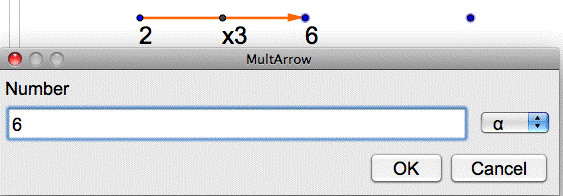
Window to type previous product

Type the new number for your new calculation.

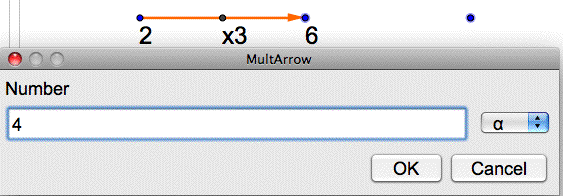
Window to type new factor

The new arrow and results will appear.

2-arrow daisy chain for 2 x 3 x 4 = 24

The DivArrow tool works the same way, only with division.
You can use fractions in your calculations; use the slash (/) character for the fraction bar. Fractions will show in the window in simplified fraction form. Note: the division sign looks a little like a + sign. There are no pluses in this activity.

Some questions to try:

  1. What is 31 x 94?
  2. What is 1/2 x 1/3?
  3. What is 1/2 divided by 1/3?
  4. What is 4 divided by 7?
  5. How could you get from 1 to 2/3 in one multiplication step and one division step, multiplying and dividing by whole numbers?
  6. How can you multiply 3/7 x 4/5 in steps of multiplying and dividing by whole numbers?
  7. How could you get from 3/4 to 2/3 in steps multiplying and dividing by whole numbers?
  8. Suppose you have a chain of multiplications and divisions. What multiplications and divisions will reverse the entire chain?

Susan Addington, Created with GeoGebra